2021학년도 수능 가형 20번 어려운 이유 & 해설
게시글 주소: https://w.orbi.kr/00033501365
2021학년도 수능 가형 20번 (by.csm).pdf
안녕하세요 CSM입니다.
20번 해설을 들고왔습니다.
현재 21번보다
체감 난이도가 높다고 여겨지는 20번입니다.
21번
체감난이도가 높은 이유는
1) 함수 g(x)의 치역설정
2) 정적분의 "결과값"을 통해 함수 개형추론
에 있어서 기존 기출에서
단단하게 연습하기 어려운 형태여서
학생들이 조금 풀기 어려워한 듯 보입니다.
먼저 교양적으로 알아야 할 사실은
아래 그림과 같이 삼각함수 반주기의
넓이(정적분값)를 빠르게 파악해야 합니다.
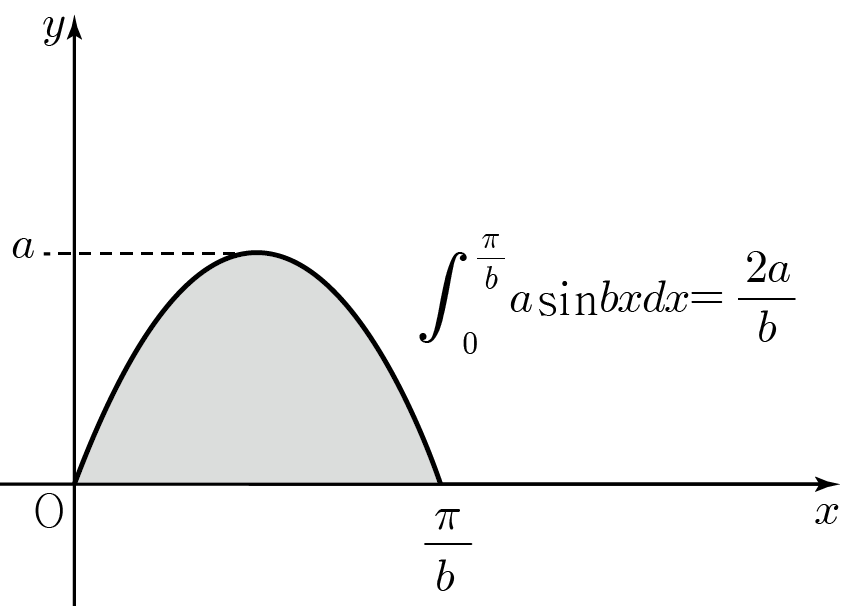
이를 토대로 해설은 다음과 같습니다. (아래 이미지 PDF도 첨부)
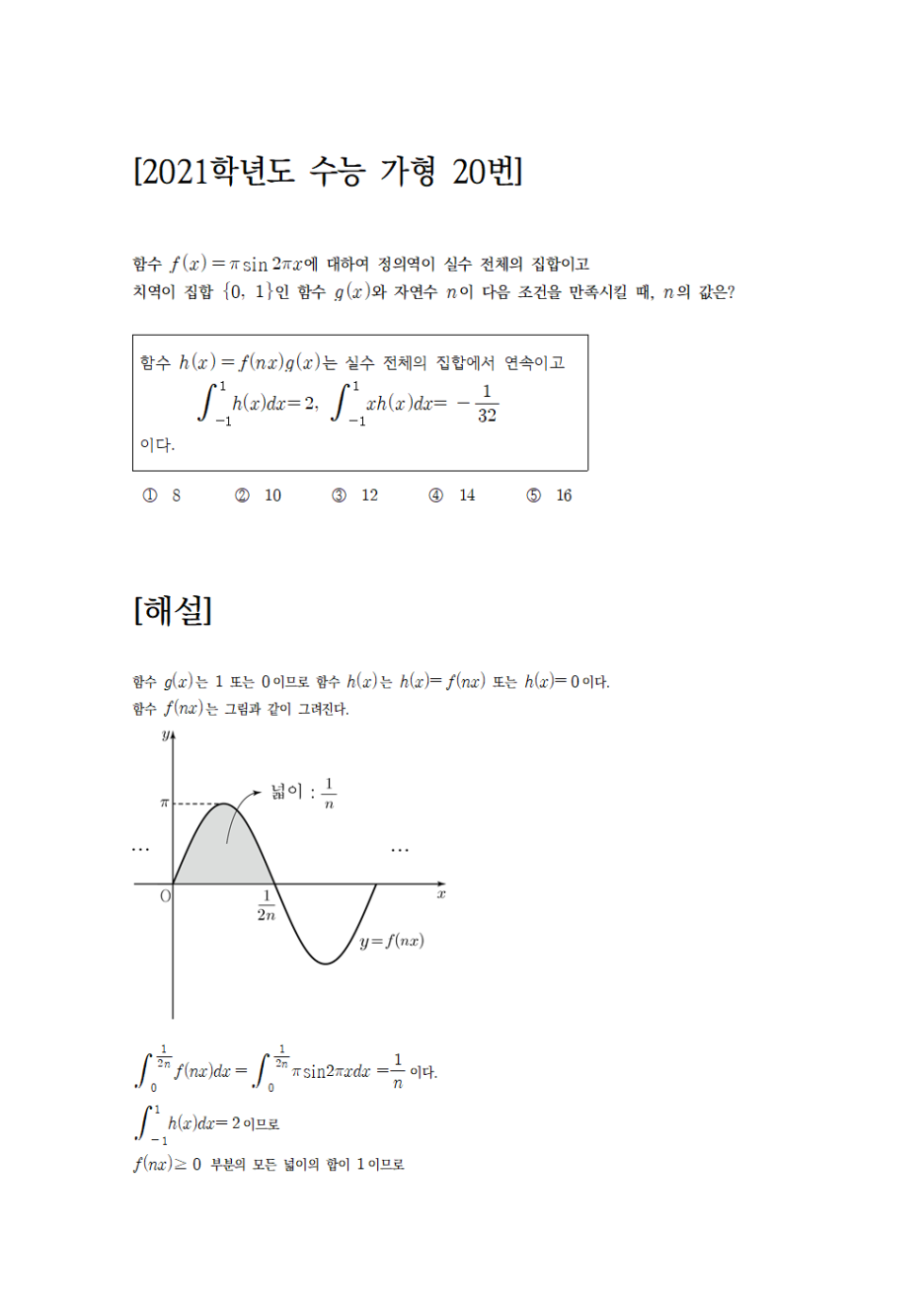
사진 설명을 입력하세요.
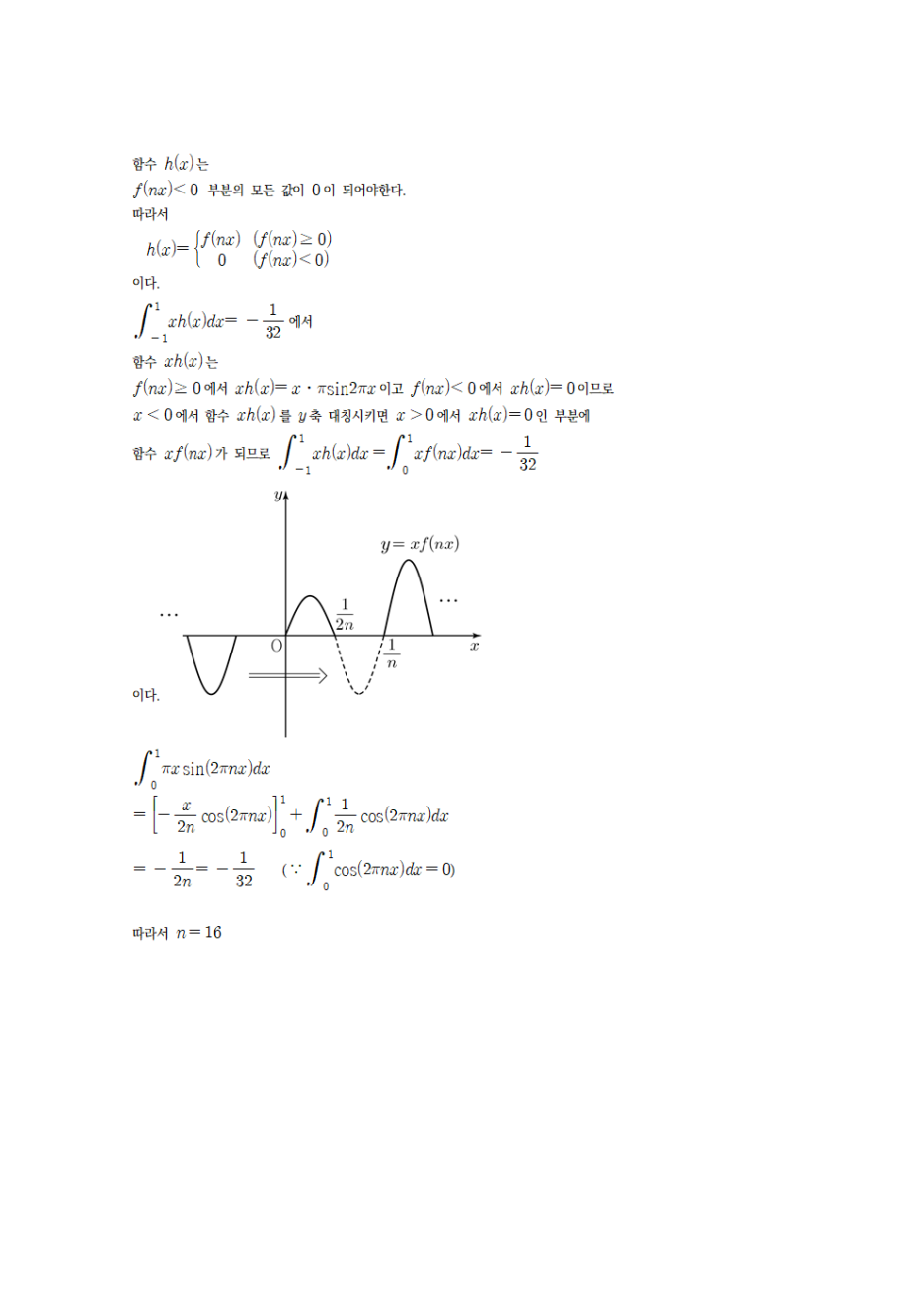
사진 설명을 입력하세요.
두가지 적분의 해석을 넓이관점과 식의 관점으로 보는 방향에 따라
풀이속도가 달라질 수 있는 문제이고 이런 경우에는
학생들에게 체감난이도 격차를 줄 수 있었던 문제라고 생각합니다.
도움이 되셨기를 바랍니다.
0 XDK (+0)
유익한 글을 읽었다면 작성자에게 XDK를 선물하세요.
-
맞팔구함뇨 6
네
-
4규원래 비쌈? 4
작년까지 2만원중반가격?으로기억하는데 갑자기 31000원..
-
성비 뭐냐뇨이 11
여친 후보가 아니라 형제자매라니까요
-
서울과학기술대학교 합격생을 위한 노크선배 꿀팁 [과기대25] [기숙사와 주변 자취 정보] 0
대학커뮤니티 노크에서 선발한 서울과학기술대학교 선배가 오르비에 있는 예비...
-
나도 뱃지를 달아보자꾸나..
-
모태솔로라니
-
이대 약대 정시 1
의약대 정시 면접없이 수능100인가요??
-
누가 제일 낫나요
-
손 ㅁㅌㅊ? 4
남르비임
-
1. 성균관대 복전 자유로운가요? 전기전자나 소프트웨어 복전 할 수 있는지...
-
올년도에 개념+3개년 기출은 했는데 사실상 기억이 잘 안남 내년부터 다시 할려고...
-
션티 프리퀀시 0
Day 당 외우는데 얼마정도의 시간이 드시나요? 파생어까지 합쳐서 외우니까 양이...
-
진짜 표본이 없어도 너무없네 특히 문과….. 심지어 산식도 바껴서 이게짠건지 후한건지도 구분이안감
-
이거 뭐임? 닉 색깔이 금색인 거
-
나만그래?
-
손 ㅇㅈ) 14
이건 찐이니 보실 분들은 보고 아닌분들은 안보셔도 되여
-
맞는 말이라도 논점과 관련없는 요소를 가지고 필자를 조롱하는 어투로 말하면 설득력이...
-
이준석 "이재명, 재판지연 움직임 수년째, 尹도 지연…자존심 센 두 바보의 대결" 21
[서울=뉴시스] 최희정 기자 = 이준석 개혁신당 의원이 "이재명 더불어민주당 대표가...
-
가군인거지 엄청 고민되네
-
지금이라도 취소해야 하나요..?ㅜ
-
왜클릭
-
갑자기 롤체를 달리기 시작한 리헨즈씨
-
환율 어지럽네 2
어카지 그냥 환전할까
-
사1과1 가산 0
사1과1 일때 과탐 가산 안주는 학교 어디어디있나요?!
-
민지야 4
-
불가능하겠죠?ㅋㅋㅋ 아 책도 다 버렸는데 어쩐담 삼반수 의미있으려면 중경외시는...
-
신나게 심찬우 쌤 강의 듣고 있었는데 갑자기 튕겼어요 계속 들어갈려고 시도하는데 창...
-
시즌초 다이아 안되겟다 이번시즌은 그.마 가야겟다
-
심심한데 의대교수나 할까?
-
연대내 학사 편입이라는 얘기도 있고 그냥 복전이라는 얘기도 있는데 뭐가맞나요?...
-
섹드립으로 들리기도 함...(평파열음화...)
-
내 앞순위에 cc많으면 좋겧네
-
안녕하세요, 오르비에서 체스라는 닉네임으로 활동을 시작하게 되었습니다. 저는...
-
고려 요소 1. 개원 후 연 1억 이상의 순이익을 안정적으로 벌 수 있는가?...
-
난 옯창이냐.
-
지금 미장 입문 어떰 12
-
언미물지 현재 고대추합할거같은데
-
한의대 합격 떴냐 12
-
4칸 고맙다!!!!
-
내 앞에 계신 모든분들 스나이핑 대박 터져서 더 좋은데로 가게해주세요. 아멘
-
중경외시 씹어먹는데 서성한은 좀 힘든 애들이 아직은 가나다군에 가고싶은 서성한만...
-
두부김치 고고혓
-
이상한 문제들 많던데 ebs 다 풀고 들어가는게 맞나요?
-
메가스터디 교재 샀는데 비닐포장도 없고 구겨저서 왔어요 책 표지 되게 이쁜데 아쉽네요
-
피램 국어 0
둘러보다가 여러번 봤는데 어떤 차별점이 있는 책임뇨..? 마닳이랑 비교해서.....
-
냥대 변표 발표 5
언제인지 아는사람?
-
아샷추는 도대체 왜 먹는거임??? 나 민초 파인애플피자 김치크림파스타 다먹는데...
-
cf)외대88퍼 중앙63퍼 경희 79퍼 시립81퍼




















































개인적으로 매우 친숙한 유형은 아니라고 생각합니다. 현장기준 어려웠을 것 같아요
asinbx 한칸넓이 a/b라서 n이 2의거듭제곱만 될거같아서 1.5중에 고민하고 5번 왼쪽정적분으로 계산해보니 사인 양수는 0곱해서 없어질것같고 음수는 -1곱해져서 양수가 될것같은 느낌으로 킹리적갓심씀
ㄹㅇ 걍 찍맞이네
아니에요 킹리적갓심은 절대 그냥 나오지 않습니다. 잘하셨습니다 ^__^
해설 잘 봤어요. 마지막에 정적분 int_{-1}^{1} xh(x)dx=int_{0}^{1} xf(nx)로 넘어가는 부분이 잘 이해가 안되는데 혹시 여유있으시다면 설명해주실 수 있을까요? 저는 사진처럼 풀었는데, 계산이 무척 더럽고 현장에서 저렇게 풀면 계산실수가 반드시 있을 것 같아서 부탁드립니다....(첫 줄의 오류는 건너뛰어주세요 고치기 귀찮아서...ㅎㅎ)
in_{-1}^{0}xh(x)dx 부분만 관찰해주시면 될 것 같습니다. 함숫값이 음수인 부분은 제거 되었을것이고 양수인부분만 남은 h(x)에 대하여 x를 곱하는데 x<0이므로 xh(x)<0가 됩니다.
따라서 xh(x)를 (-1,1)에서 그린 후 각각 적분을 하여도 괜찮습니다만,
(-1,0)인 부분을 그대로 y축 대칭시켜보면 결국 xf(nx)가 완성된다는 것을 알 수 있습니다.
이는 f(nx)가 처음부터 대칭함수이고 x를 곱하여서 '대칭성질'이 남아있다고 생각하여 판단할 수 있으며 이를 (-1, 0) => (0, 1)로 이동하는 치환적분하여 식적으로도 설명가능하나 이를 계산으로 의도하기보다는 최근 "영역관찰"을 포인트 잡아왔기에 그림도 적절히 섞어서 확인해주시면 될 것 같습니다.^^
아아아아 다 그대로 대칭되니까 그렇겠네요 감사합니다.
찍는게 더 빠를 듯. 2랑 1/32 나오고 f(nx) 주기가 1/n 이니까 8, 16 처럼 2의 거듭제곱꼴로 나오는 수가 답일 것 같고 8은 너무 작아서 16했는데 아.. 계산이 엄청 빡센거였네요
진짜 시험장에서 제일 어려웠어요... 30 20 이 최고봉.
이제 21 29 은 킬러 아닌듯해여ㅜ
와.. 그냥 1/2n~1/n, 1/n~3/2n 계속 적분해가면서 귀납적으로 적분값을 찾아냈는데 y축대칭하면 한번의 적분으로 풀리네요 진짜 충격이네