[에라둔] 역학 문항에서의 미래와 과거
게시글 주소: https://w.orbi.kr/00069303116
계산적으로 중요한 내용들은 아니고 그냥 편히 읽으시면 될법한 내용들입니다.
역학 문항을 풀다 보면 여러가지 상황을 마주하게 되는데
종종 동일한 카테고리를 마주하게 됩니다.
이번에 다룰 내용은 어찌보면은 상대속도와 조금 관련이 있을 수 있습니다만 일단 접어두고.
아래 문항들의 공통점이 무엇일까요?
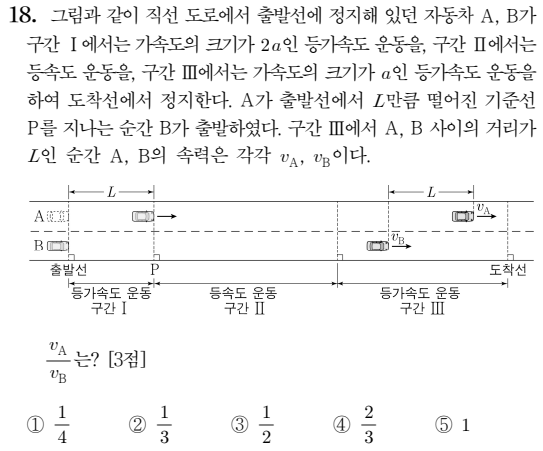

20230618


20210911


20130920
세 문항의 공통점은 두 물체가 모든 지점에 대하여 운동 방향, 속력 모든것이 동일한 상황들입니다.
이전에 저도 문항 출제를 할 때 위와 같은 상황을 이용하여 문항 출제롤 하곤 했는데
위와 같은 문항을 출제하면 참 좋은게 v-t그래프를 옆으로만 삭 밀어주면 되기 때문에
검토하기가 수월해서 즐겨냈었던 기억이 어렴풋이 납니다.
거두절미하고
어떻게 보면 위와 같은 문항들은 상대속도를 활용할만한 문항들 중에서도 특수한 케이스라고 생각을 하는데
저같은 경우에는 두 물체에 대하여 가상의 시간차 t를 가정하고 문제 풀이를 하는것을 선호합니다.
뿐만 아니라, 시간차 t가 난다고 생각하고 문항을 바라보면 좀더 문제 상황을 직관적으로 파악하기도 좋지요.


예를 들어 위 문항의 경우엔 B의 2초 뒤 모습이 A라고 생각하면서 풀면 문제 풀이가 아마 수월하겠죠.
일단 ㄱ이 바로 나올것이며
2초뒤 B가 정지할테니 평균속력 2라는 점에서 v=4가 바로 나올것이며
dv=4인동안의 시간이 2초니 가속도가 2인것도 술술 나올것입니다.


20210911
마찬가지로 위 문항도 B가 t초뒤의 A모습이라고 가정한다면 3vt=L이 나올것이며
우리는 자연스레 A가 p에서 q까지 이동하는데 걸리는 시간이 t라고 할것이기에
평균 속력 공식을 이용하여 1.5vt=0.5L과 같이 문항들이 순둥순둥하게 풀릴것입니다.
위와같이 동일한 경로, 운동 상황을 공유하는 문항의 경우에는 결국엔 대부분 문항에서 요구하는것은
두 상황에 대한 연립일것이며, 이 연립과정이 가감의 과정이기 떄문에
사실 t로 두고 문항을 풀면 쉽게 풀리는 경우가 많습니다.


20230618
위 문항의 경우에도 마찬가지로 역시 B의 t후 모습이 A라 생각하고 풀면 풀기가 수월할것입니다.
등가속도 운동 구간 I에서의 가속도를 2a라 하면 (0+2at)t/2=att=L이 나올것이며
이후 vb인 B가 시간 t 후 속력이 va가 된다고 하면 자연스레 (va+vb)/2 * t = L이 나오게 될것입니다.
그리고 구간 3에서 시간 t동안 속력이 변하였는데 이것이 va-vb일지 vb-va일지는 잘 모르겠습니다.
사실 시간 t라는 차이를 생각해보면 B가 출발할 때 이미 가속된 A가 있기에 거리차가 L보다 벌어질텐데
다시 L로 감소했다는 포인트를 보면 아마 가속도가 감소했음을 알기 수월하겠지요.
그러한 이유로 (va+vb)=2L/t, (vb-va)=at=L/t
va+vb : vb-va = 2:1, 2vb-2va = va+vb, 3va=vb, va:vb=1:3 이 나오게 될것입니다.
저같은 경우에는 두 물체가 동일한 경로를 운동하면 습관적으로 동일한 운동까지 하는지를 체크합니다.
아마 위와같은 유형들을 깔끔하게 푸시는 분들이라면 위의 개념을 숙지한 상태에서
그 이상은 본인의 직관, 암산 등으로 인한 최적화 정도의 차이만이 존재할것입니다.
만약, 위와 같은 수식적 풀이가 다소 어렵다면 그냥 모든 시간 영역을 t미지수로 두고 풀어보시거나
vt 그래프를 정성스럽게 그려보시는것을 권장드립니다.
아마 그래프를 그리시다 보면 자연스레 평행사변형과 친해지게 될겁니다.
0 XDK (+0)
유익한 글을 읽었다면 작성자에게 XDK를 선물하세요.
-
오늘 구매하신 분들 해설에 집중해서 공부하고 가세용~~ 해설도 기출 아닌 것들은...
-
그 길이랑 단면적에 저항 비례 반비례하는거랑 피스톤 열역학 이거 출제 자주됐음?...
-
일탈행동이 발생하는 과정에서 나타나는 상호작용을 중시 차교론 2
낙인론 둘다 되죠?
-
상향평준화돼서 47~48 뜨려나
-
ㄹㅈㄷ인점 4
비타민인줄 알고 샀는데 하...
-
따로 말씀 안 드리고 적어도 되죠?? 가채점표 안 붙이면요
-
오랜만입니다 3
응원해요 항상
-
역학적에너지 3번은 또 뭐냐?
-
샤프고장나면 대처법) 20
컴싸로 풀면 됨
-
ㅈㄱㄴ
-
끝나고 대기하는동안 채점하면 눈물날거같은데
-
샤프 고장났을 때 멘탈 대처해야지. 수능샤프 내구성 생각보다 시발임.
-
하 이거땜에 탐구 고인듯.. 왜 내가 수능볼때
-
수능 잘보고 오세요! 원의 방정식 파트는 두번째것만 봐도 무방할 듯 합니다 수학 하...
-
26번은 어디임? 네이버에 쳐봐도 위치가 다 다름 ..ㅋㅋ
-
시계 지우개 수험표 민증 밥 예열지문 샤프심 끝?
-
사문 하… 내가못하는거겟지
-
쉬는 시간 아니고 텀있을때 감독관님께 말히면 보내주나요?? 그리고 만약에 시험도중...
-
재발
-
시작
-
초침소리남 이거 ㄱㅊ?
-
영어 짝수 질문 1
문맥상 맞는거 찾는30번 문제 있진항. 그거 막 답 바꿔서 내고 그러진 않지?
-
화작 ㅅㅂ 4
표점 깎여도 좀 스근하게 할려고 골랐더만 작년 9월부터 왜이리 어렵게 내는거냐;;...
-
반도체 imf sdr 아웃소싱
-
사문 하수 질문 1
사문 하수라 평가원 3 아슬아슬 하게 뜨는데 적중예감 진짜 더럽게 어렵더라고요그냥...
-
까짓거 수능 얼마나 중요하다고 에혀 내일 잘 못봐도 되니까 실수만 하지말자 ㅈㅂ!!!
-
짝수+15km 0
걸어가면 3시간 50분ww 헤헤 잘보고와야지
-
240621수학만봐도.
-
사문연습) A가 진화론이면 (가)에는 ~가 들어갈 수 없다 4
적중예감 풀면서 시험지 찢고 싶게 하는 문제 1위
-
다들 폰 보면서 조용하게 기다리는게 ㄹㅇ.........
-
내일 시험끝나면 털많은 고양이 수인한테 나데나데 받고싶다 3
여러분들 화이팅입니다
-
가보자!!
-
마음을 비우자 1
실수여부는 하늘이 점지해주는 것 난 다만 최선을 다할 뿐
-
어 이게 자연현사잉었나? 아닌가 사문현상인가? 안이랬는데..
-
동국대 근황 4
동덕대랑 헷갈림 당함 ㅜㅜ 동평 개빡치네
-
국제 사법 재판소는 직접제재를 할수없고 대신에 안보리가 직접제재를 할수있는건가요?
-
최대 최소의 합 0
순서쌍의개수
-
제일좋아하는자리에누워
-
표독한 유키 보고가 15
냥
-
민지가 내일 수능 잘 보래요
-
이제 예비소집 빡세네 10
10년 전엔 교실 앞까지 가보고 11년 전엔 교실 들어가서 내 자리 미리...
-
쓰고 나오면 몇시에요?
-
미적 28번 1
올해 미적 28번은 또 2번????
-
다들 막 26수능 경쟁률 전년도 수능보다 훨 높고 정시에만 매달려서 대학가려면...
-
책상에 시험지랑 시계랑 여러가지 놓으면 간식이랑 텀블러 놓을 자리가 없던데 어디다...
-
멀 먹어야 잘 먹었다고 소문이 날까요
-
그래그래 맞아, 에타만든 사람이 연머생이라 그래. 기습연혐.
-
ㅇㅇ

















































옆동네 옆옆동네에서 잘 보고 있습니다감사합니다!!
와 쌤 과외 받았던 학생인데,,, 잘 계시나요 ㅠㅠ
감사했습니다!! 덕분에 카이스트 가서 잘 지내고있어요